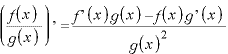§２演習問題B（p.92）

教科書外の公式は書きませんのでそのつもりで．

[@]

1. 次の関数の増減を調べよ．

[@]

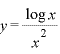
（1） $y=\displaystyle \frac{\log x}{x^{2}}$

解

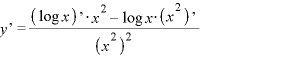$y'=\displaystyle \frac{\left(\log x\right)'\cdot x^{2}-\log x\cdot\left(x^{2}\right)'}{\left(x^{2}\right)^{2}}$ ※１

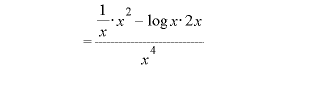$=\displaystyle \frac{\frac{1}{x}\cdot x^{2}-\log x\cdot 2x}{x^{4}}$ ※２，３

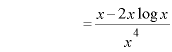
$=\displaystyle \frac{x-2x\log x}{x^{4}}$

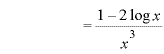
$=\displaystyle \frac{1-2\log x}{x^{3}}$

$\text{[math]}$ ∴ $x\neq 0$

$y'=0$ の時、

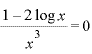
$\displaystyle \frac{1-2\log x}{x^{3}}=0$

$1-2\log x=0$

$\displaystyle \log x=\frac{1}{2}$

$x=[NapierNumber]^{\frac{1}{2}}$

$x=\sqrt{[NapierNumber]}$

$x=\sqrt{[NapierNumber]}$ の時、

$y=\displaystyle \frac{\log\sqrt{[NapierNumber]}}{\left(\sqrt{[NapierNumber]}\right)^{2}}$

$=\displaystyle \frac{\frac{1}{2}\log[NapierNumber]}{e}$

$=\displaystyle \frac{1}{2[NapierNumber]}$

増減表を書く．

$\text{[math]}$


-	+	0	-
?	?		?

$\text{[math]}$ ∴ $0<x<\sqrt{[NapierNumber]}$ の時増加、 $0>x,x>\sqrt{[NapierNumber]}$ の時減少する．

使用公式

※１　商の微分

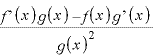
$\left(\frac{f\left(x\right)}{g\left(x\right)}\right)$ ?= $\displaystyle \frac{f'\left(x\right)g\left(x\right)-f\left(x\right)g'\left(x\right)}{g\left(x\right)^{2}}$

※２

$\left(\log x\right)$ ?= $\displaystyle \frac{1}{x}$

$\text{※３}$

$a,b$ $\text{は定数．}$

$\left(ax^{b}\right)'=abx^{b-1}$

[@]

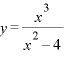
（2） $y=\displaystyle \frac{x^{3}}{x^{2}-4}$

解

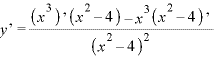$y'=\displaystyle \frac{\left(x^{3}\right)'\left(x^{2}-4\right)-x^{3}\left(x^{2}-4\right)'}{\left(x^{2}-4\right)^{2}}$ ※１

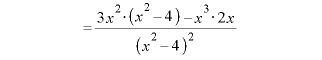$=\displaystyle \frac{3x^{2}\cdot\left(x^{2}-4\right)-x^{3}\cdot 2x}{\left(x^{2}-4\right)^{2}}$ ※２

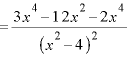
$=\displaystyle \frac{3x^{4}-12x^{2}-2x^{4}}{\left(x^{2}-4\right)^{2}}$

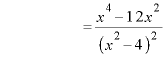
$=\displaystyle \frac{x^{4}-12x^{2}}{\left(x^{2}-4\right)^{2}}$

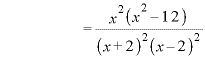
$=\displaystyle \frac{x^{2}\left(x^{2}-12\right)}{\left(x+2\right)^{2}\left(x-2\right)^{2}}$

$\text{[math]}$ ∴ $x\neq\pm 2$

$y'=0$ の時、

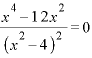
$\displaystyle \frac{x^{4}-12x^{2}}{\left(x^{2}-4\right)^{2}}=0$

$x^{4}-12x^{2}=0$

$x^{2}\left(x^{2}-12\right)=0$

$x^{2}\left(x+2\sqrt{3}\right)\left(x-2\sqrt{3}\right)=0$

$\text{[math]}$ ∴ $x=0,\pm 2\sqrt{3}$

$x=0,\pm 2\sqrt{3}$ の時、

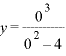
$y=\displaystyle \frac{0^{3}}{0^{2}-4}$

$=0$

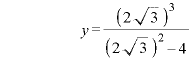
$y=\displaystyle \frac{\left(2\sqrt{3}\right)^{3}}{\left(2\sqrt{3}\right)^{2}-4}$

$\text{[math]}$ $=\displaystyle \frac{24\sqrt{3}}{12-4}$

$\text{[math]}$ $=\displaystyle \frac{24\sqrt{3}}{8}$

$\text{[math]}$ $=4\sqrt{3}$

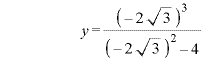
$y=\displaystyle \frac{\left(-2\sqrt{3}\right)^{3}}{\left(-2\sqrt{3}\right)^{2}-4}$

$=-\displaystyle \frac{24\sqrt{3}}{12-4}$

$=-\displaystyle \frac{24\sqrt{3}}{8}$

$=-4\sqrt{3}$

$\text{[math]}$ 増減表を作成

			-2				2
+	0	-		-	0	-		-	0	+
?		?		?	0	?		?		?

$\text{[math]}$ ∴ $-2\sqrt{3}>x,x>2\sqrt{3}$ の時、増加、 $-2\sqrt{3}<x<-2,-2<x<2,2<x<2\sqrt{3}$ の時、減少する．

使用公式

$\text{[math]}$ ※１　商の微分

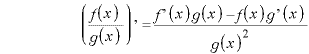
$\displaystyle \left(\frac{f\left(x\right)}{g\left(x\right)}\right)'=\frac{f'\left(x\right)g\left(x\right)-f\left(x\right)g'\left(x\right)}{g\left(x\right)^{2}}$

$\text{[math]}$ ※２

$a,b$ $\text{は定数．}$

$\left(ax^{b}\right)'=abx^{b-1}$

[@]

（3） $y=\displaystyle \frac{x}{\sqrt[3]{}\left(x-1\right)^{2}}$

解

$y'=\displaystyle \frac{\left(x\right)'\cdot\sqrt[3]{\left(x-1\right)^{2}}-x\cdot\left(\sqrt[3]{\left(x-1\right)^{2}}\right)'}{\left(\sqrt[3]{\left(x-1\right)^{2}}\right)^{2}}$ ※１

$=\displaystyle \frac{\sqrt[3]{\left(x-1\right)^{2}}-x\left(\left(x-1\right)^{\frac{2}{3}}\right)'}{\sqrt[3]{\left(x-1\right)^{4}}}$ ※２

$=\displaystyle \frac{\sqrt[3]{\left(x-1\right)^{2}}-x\cdot\frac{2}{3}\left(x-1\right)^{-\frac{1}{3}}\cdot\left(x-1\right)'}{\sqrt[3]{\left(x-1\right)^{4}}}$ ※３，２

$=\displaystyle \frac{\sqrt[3]{\left(x-1\right)^{2}}-\frac{2x}{3\sqrt[3]{x-1}}}{\sqrt[3]{\left(x-1\right)^{4}}}$ ※２

$=\displaystyle \frac{\sqrt[3]{\left(x-1\right)^{3}}-\frac{2}{3}x}{\sqrt[3]{\left(x-1\right)^{5}}}$

$=\displaystyle \frac{x-1-\frac{2}{3}x}{\left(x-1\right)\sqrt[3]{\left(x-1\right)^{2}}}$

$=\displaystyle \frac{\frac{1}{3}x-1}{\left(x-1\right)\sqrt[3]{\left(x-1\right)^{2}}}$

$=\displaystyle \frac{x-3}{3\left(x-1\right)\sqrt[3]{\left(x-1\right)^{2}}}$

$\text{[math]}$ ∴ $x\neq 1$

$y'=0$ の時、

$\displaystyle \frac{x-3}{3\left(x-1\right)\sqrt[3]{\left(x-1\right)^{2}}}=0$

$x-3=0$

$x=3$

$x=3$ の時、

$y=\displaystyle \frac{3}{\sqrt[3]{\left(3-1\right)^{2}}}$

$=\displaystyle \frac{3}{\sqrt[3]{2^{2}}}$

$=\displaystyle \frac{3}{\sqrt[3]{4}}$

$=\displaystyle \frac{3\sqrt[3]{2}}{2}$

$\text{[math]}$ 増減表を書く．

	1		3
+		-	0	+
?		?		?

$\text{[math]}$ ∴ $1>x,x>3$ で増加、 $1<x<3$ で減少する．

使用公式

※１　商の微分

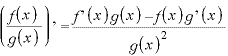
$\displaystyle \left(\frac{f\left(x\right)}{g\left(x\right)}\right)'=\frac{f'\left(x\right)g\left(x\right)-f\left(x\right)g'\left(x\right)}{g\left(x\right)^{2}}$

$\text{[math]}$ ※２

$a,b$ $\text{は定数．}$

$\left(ax^{b}\right)'=abx^{b-1}$

※３　合成関数

$\left(f\left(g\left(x\right)\right)\right)'=f'\left(g\left(x\right)\right)g'\left(x\right)$

[@]

2. 微分可能な関数 $f\left(x\right)$ に対して、方程式 $f\left(x\right)=0$ は異なる実数解 $\alpha,\beta$ をもつとする．方程式 $f'\left(x\right)=0$ は $\alpha$ と $\beta$ の間に少なくとも１つの実数解をもつことを示せ．

解

証明）

$f\left(\alpha\right)=0=f\left(\beta\right)$

∴ロルの定理より、※１

$f'\left(x\right)=0$ の実数解が存在する．Q.E.D.

使用公式

※１　ロルの定理

関数 $f\left(x\right)$ が閉区間 $[a,b]$ で連続であり、開区間 $(a,b)$ で微分可能であるとする．さらに、 $f\left(a\right)=f\left(b\right)$ であれば、

$f'\left(c\right)=0 , a<c<b$

$\text{[math]}$ となる数 $c$ が少なくとも１つ存在する．

[@]

3. 関数 $f\left(x\right)=x^{3}$ について、次の関係式をみたす $\theta$ の極限 $\displaystyle \lim_{h\rightarrow 0}\theta$ を求めよ．

$f\left(a+h\right)=f\left(a\right)+f'\left(a+\theta h\right)h\left(a\neq 0, & 0<\theta<1\right)$

解

$f'\left(x\right)=3x^{2}$ ※１

$\left(a+h\right)^{3}=a^{3}+3\left(a+\theta h\right)^{2}h$

$a^{3}+3a^{2}h+3ah^{2}+h^{3}=a^{3}+3\left(a^{2}+2a\theta h+\theta^{2}h^{2}\right)h$

$a^{3}+3a^{2}h+3ah^{2}+h^{3}=a^{3}+3a^{2}h+6a\theta h^{2}+3\theta^{2}h^{3}$

$3a^{2}h+3ah^{2}+h^{3}=3a^{2}h+6a\theta h^{2}+3\theta^{2}h^{3}$

$3a^{2}+3ah+h^{2}=3a^{2}+6a\theta h+3\theta^{2}h^{2}$

$3ah+h^{2}=6a\theta h+3\theta^{2}h^{2}$

$3a+h=6a\theta+3\theta^{2}h$

$3\theta^{2}h+6a\theta-3a-h=0$

$\text{[math]}$ この式の極限をとる．

$\displaystyle \lim_{h\rightarrow 0}3\theta^{2}h+6a\theta-3a-h=0$

$6a\theta-3a=0$

$\displaystyle \theta=\frac{1}{2}$

$\text{[math]}$ ∴ $\displaystyle \lim_{h\rightarrow 0}\theta=\frac{1}{2}$

使用公式

$\text{[math]}$ ※１

$a,b$ は定数．

$\left(ax^{b}\right)'=abx^{b-1}$

[@]

4. $\displaystyle \lim_{x\rightarrow\infty}f'\left(x\right)=a$ のとき、等式 $\displaystyle \lim_{x\rightarrow\infty}\left\{f\left(x+3\right)-f\left(x\right)\right\}=3a$ を証明せよ．

解

証明） $f'\displaystyle \left(x\right)=\lim_{h\rightarrow 0}\frac{f\left(x+h\right)-f\left(x\right)}{h}$

$\text{[math]}$ ∴ $\displaystyle \lim_{h\rightarrow 0}hf'\left(x\right)=\lim_{h\rightarrow 0}f\left(x+h\right)-f\left(x\right)$

$hf'\left(x\right)=f\left(x+h\right)-f\left(x\right)$

$\displaystyle \lim_{x\rightarrow\infty}hf'\left(x\right)=\lim_{x\rightarrow\infty}\left\{f\left(x+h\right)-f\left(x\right)\right\}$

$h\displaystyle \lim_{x\rightarrow\infty}f'\left(x\right)=\lim_{x\rightarrow\infty}\left\{f\left(x+h\right)-f\left(x\right)\right\}$

$\text{[math]}$ ∴ $3a=\displaystyle \lim_{x\rightarrow\infty}\left\{f\left(x+3\right)-f\left(x\right)\right\}$

使用公式

[@]

5. 関数 $\sin\left(x+\frac{\pi}{6}\right)$ について、 $\left|x\right|$ は十分小さいとする．

[@]

（1）　この関数の近似式 $ax+b$ を求めよ．

解

$f\left(x\right)=\sin\left(x\right)$ とすると、

$f'\left(x\right)=\cos x$ ※１

近似式を求める．

$f\left(x+\frac{\pi}{6}\right)=f\left(\frac{\pi}{6}\right)+f'\left(\frac{\pi}{6}\right)x$ ※２

$=\displaystyle \sin\frac{\pi}{6}+\cos\frac{\pi}{6}x$

$=\displaystyle \frac{1}{2}+\frac{\sqrt{3}}{2}x$

$\text{[math]}$ ∴ $\displaystyle \frac{\sqrt{3}}{2}x+\frac{1}{2}$

使用公式

※１

$\left(\sin x\right)'=\cos x$

※２　近似

$f\left(x+dx\right)\fallingdotseq f\left(x\right)+f'\left(x\right)h$

[@]

（2）　前問を用い、 $\sin 29$ ° の近似値を小数第３位まで求めよ．

解

$\sin 29$ ° $=\sin\left(\frac{\pi}{6}-\frac{\pi}{180}\right)$

$\text{[math]}$ ∴ 近似値は、

$\displaystyle \frac{1}{2}-\frac{\sqrt{3}}{2}\cdot\frac{\pi}{180}=0.5-\frac{\pi\sqrt{3}}{360}$

$=0.5-0.015$

$=0.485$

使用公式

[@]

6. $0<x<\displaystyle \frac{1}{2}$ に対して、次の不等式が成り立つことを示せ．

$\displaystyle \log\frac{1+x}{1-x}<2x+\frac{2}{3}x^{3}+\frac{8}{15}x^{5}$

解

$f\displaystyle \left(x\right)=2x+\frac{2}{3}x^{3}+\frac{8}{15}x^{5}-\log\frac{1+x}{1-x}$ とおく．

$f'\displaystyle \left(x\right)=2+2x^{2}+\frac{8}{3}x^{4}-\left(\log\frac{1+x}{1-x}\right)'$ ※１

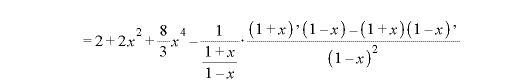$=2+2x^{2}+\displaystyle \frac{8}{3}x^{4}-\frac{1}{\frac{1+x}{1-x}}\cdot\frac{\left(1+x\right)'\left(1-x\right)-\left(1+x\right)\left(1-x\right)'}{\left(1-x\right)^{2}}$ ※２、３

$=2+2x^{2}+\displaystyle \frac{8}{3}x^{4}-\frac{1-x+}{\left(1+x\right)\left(1-x\right)}$

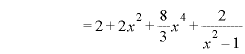
$=2+2x^{2}+\displaystyle \frac{8}{3}x^{4}+\frac{2}{x^{2}-1}$

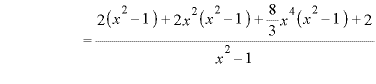
$=\displaystyle \frac{2\left(x^{2}-1\right)+2x^{2}\left(x^{2}-1\right)+\frac{8}{3}x^{4}\left(x^{2}-1\right)+2}{x^{2}-1}$

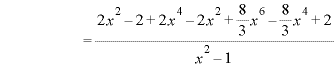
$=\displaystyle \frac{2x^{2}-2+2x^{4}-2x^{2}+\frac{8}{3}x^{6}-\frac{8}{3}x^{4}+2}{x^{2}-1}$

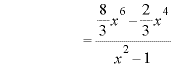
$=\displaystyle \frac{\frac{8}{3}x^{6}-\frac{2}{3}x^{4}}{x^{2}-1}$

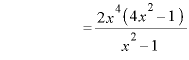
$=\displaystyle \frac{2x^{4}\left(4x^{2}-1\right)}{x^{2}-1}$

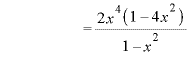
$=\displaystyle \frac{2x^{4}\left(1-4x^{2}\right)}{1-x^{2}}$

$\left[0,\frac{1}{2}\right]$ で $1-4x^{2}>0,1-x^{2}>0$

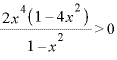
$\text{[math]}$ ∴ $\displaystyle \frac{2x^{4}\left(1-4x^{2}\right)}{1-x^{2}}>0$

$f\displaystyle \left(0\right)=2\cdot 0+\frac{2}{3}\cdot 0^{3}+\frac{8}{15}\cdot 0^{5}-\log\frac{1+0}{1-0}$

$=-\log 0$

$=0$

$\text{[math]}$ ∴ $f\left(x\right)$ は $\left[0,\frac{1}{2}\right]$ で増加し、 $f\left(0\right)=0$ 　なので式は成り立つ．

使用公式

$\text{[math]}$ ※１

a,b は定数．

$\left(ax^{b}\right)$ ?=ab $x^{b-1}$

※２　合成関数

$\left(f\left(g\left(\right)\right)\right)'=f'\left(g\left(x\right)\right)g'\left(x\right)$

※３　商の微分

$\displaystyle \left(\frac{f\left(x\right)}{g\left(x\right)}\right)'=\frac{f'\left(x\right)g\left(x\right)-f\left(x\right)g'\left(x\right)}{g\left(x\right)^{2}}$