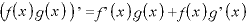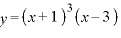
§3演習問題B(p.106)
教科書外の公式は書きませんのでそのつもりで.
[@]
1. 次の関数の極地を求めよ.
[@]
(1) 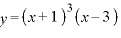
解
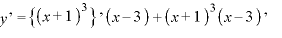 ※1
※1
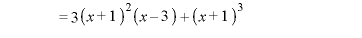 ※2,3
※2,3
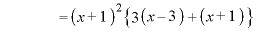
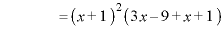
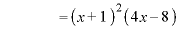
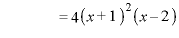
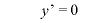 のとき、
のとき、
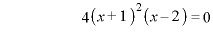
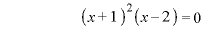
 ∴
∴ 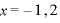
 ∴
∴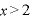 のとき、増加
のとき、増加 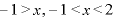 のとき、減少(皆は増減表を書きましょう。俺は面倒だからパス。)
のとき、減少(皆は増減表を書きましょう。俺は面倒だからパス。)
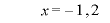 のとき、
のとき、
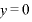
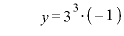
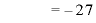
∴ 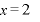 のとき、極小
のとき、極小 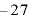
使用公式
※1 積の微分
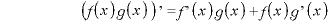
※2 合成関数
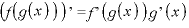
 ※3
※3
 は定数.
は定数.
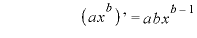
[@]
(2) 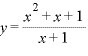
解
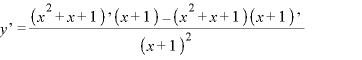 ※1
※1
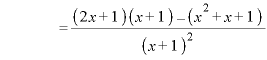
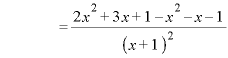
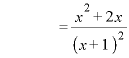
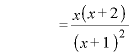
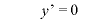 のとき、
のとき、
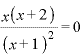
 ∴
∴ 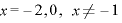
 ∴
∴ 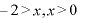 のとき増加
のとき増加 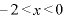 のとき減少(皆は増減表を書きましょう。俺は面倒だからパス。)
のとき減少(皆は増減表を書きましょう。俺は面倒だからパス。)
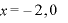 のとき、
のとき、
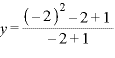
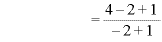




 ∴
∴ 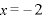 極大
極大 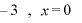 極小
極小 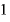
使用公式
※1 商の微分
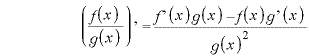
[@]
(3) ![y=\displaystyle \frac{x}{\sqrt[3]{x}-1}](./6_images/math052.png)
解
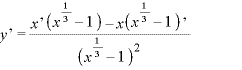 ※1
※1
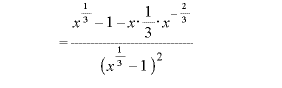 ※2
※2
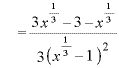
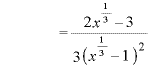
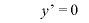 のとき、
のとき、
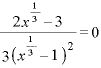
 ∴
∴ 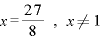
 ∴
∴ 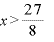 のとき増加
のとき増加 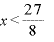 のとき減少(皆は増減表を書きましょう。俺は面倒だからパス。)
のとき減少(皆は増減表を書きましょう。俺は面倒だからパス。)
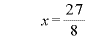 のとき、
のとき、
![y=\displaystyle \frac{\frac{27}{8}}{\sqrt[3]{\frac{27}{8}}-1}](./6_images/math065.png)
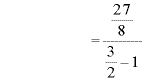
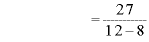

 ∴
∴ 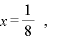 極小
極小 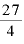
使用公式
※1 商の微分
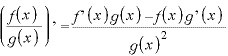

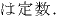
[@]
(4) 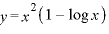
解
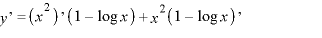 ※1
※1
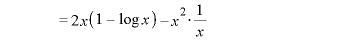 ※2,3
※2,3
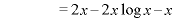
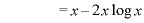
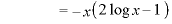
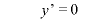 のとき、
のとき、
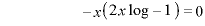
 ∴
∴ ![x=0,\sqrt{[NapierNumber]}](./6_images/math086.png)
 ∴
∴ ![0<x<\sqrt{[NapierNumber]}](./6_images/math088.png) のとき増加
のとき増加 ![\sqrt{[NapierNumber]}<x](./6_images/math089.png) のとき減少(皆は増減表を書きましょう。俺は面倒だからパス。)
のとき減少(皆は増減表を書きましょう。俺は面倒だからパス。)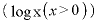
※3
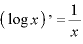

![x=\sqrt{[NapierNumber]}](./6_images/math093.png) のとき、
のとき、
![y=\sqrt{[NapierNumber]}^{2}\left(1-\log\sqrt{e}\right)](./6_images/math094.png)
![=[NapierNumber]\left(1-\frac{1}{2}\log[NapierNumber]\right)](./6_images/math095.png)
![=[NapierNumber]\left(1-\frac{1}{2}\right)](./6_images/math096.png)
![=\displaystyle \frac{[NapierNumber]}{2}](./6_images/math097.png)
 ∴
∴ ![x=\sqrt{[NapierNumber]}](./6_images/math099.png) , 極大
, 極大 ![\displaystyle \frac{[NapierNumber]}{2}](./6_images/math100.png)
使用公式
※1 積の微分
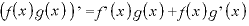
 ※2
※2
 は定数.
は定数.
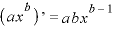
 ※3
※3
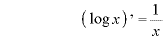
[@]
(5) 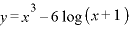
解
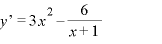 ※1
※1
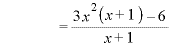
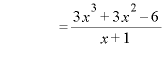
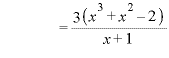
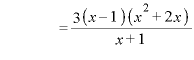
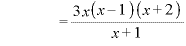
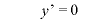 のとき、
のとき、
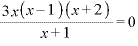
 ∴
∴ 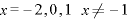
 ∴
∴ 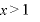 のとき増加
のとき増加 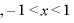 のとき減少(皆は増減表を書きましょう。俺は面倒だからパス。)
のとき減少(皆は増減表を書きましょう。俺は面倒だからパス。)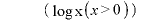
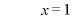 のとき、
のとき、
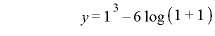
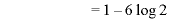
 ∴
∴ 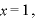 極小
極小 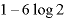
使用公式
※1
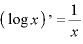
[@]
2. 関数 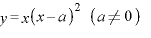 が極大になるグラフ上の点
が極大になるグラフ上の点 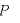 の座標を
の座標を 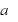 で表せ.また、
で表せ.また、 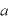 が変化するとき、点
が変化するとき、点 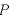 の軌跡を図示せよ.
の軌跡を図示せよ.
解
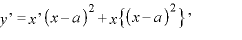 ※1
※1
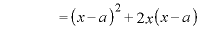
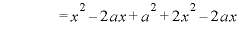
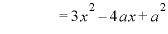
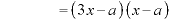
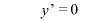 のとき、
のとき、
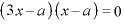
 ∴
∴ 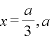
 ∴
∴ 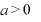 のとき、
のとき、
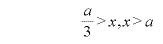 増加
増加 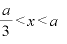 減少
減少
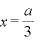 のとき、
のとき、
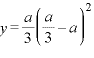
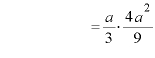
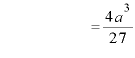
 ∴
∴ 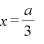 のとき 極大
のとき 極大 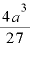
 ∴
∴ 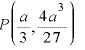



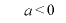 のとき、
のとき、
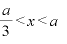 増加
増加 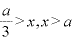 減少
減少
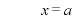 のとき、
のとき、
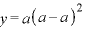

 ∴
∴ 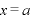 のとき 極大
のとき 極大 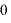
 ∴
∴ 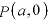

使用公式
※1 積の微分